Дифференциальная цепь схема. Цепи формирования сигнала. Дифференцирующая и интегрирующая цепь. Условия дифференцирования и интегрирования

Лабораторная работа

«Дифференцирующие и интегрирующие цепи»

Полянчев С., Коротков Р.

Цели работы: ознакомление с принципом действия, основными свойствами и параметрами дифференцирующих и интегрирующих цепей, установление условия дифференцирования и интегрирования, определение постоянной времени.

Теоретическая часть.

В радиоэлектронике и экспериментальной физике возникает необходимость преобразования формы сигналов. Часто это может быть выполнено путём их дифференцирования или интегрирования. Например, при формировании запускающих импульсов для управления работой ряда устройств импульсной техники (дифференцирующие цепи) или при выделении полезного сигнала на фоне шумов (интегрирующие цепи).

Анализ простейших цепей для дифференцирования и интегрирования сигналов

Дифференцирующей называется радиотехническая цепь, с выхода которой может сниматься сигал, пропорциональный производной от входного сигнала U вых (t) ~ dU вх (t)/dt(1)

Аналогично, для интегрирующей цепи: U вых (t) ~ òU вх (t)dt(2)

Поскольку дифференцирование и интегрирование являются линейными математическими операциями, указанные выше преобразования сигналов могут осуществляться линейными цепями, т.е. схемами, состоящими из постоянных индуктивностей, емкостей и сопротивлений.

Рассмотрим цепь с последовательно соединёнными R, C и L, на вход которой подаётся сигал U вх (t) (рис.1).

Выходной сигал в такой цепи можно снимать с любого её элемента. При этом:

U R +U C +U L = Ri(t) + 1/c òi(t)dt + L di(t)/dt = U вх (t). (3)

Очевидно, что поскольку значения U R , U C и U L определяются параметрами R, C и L, то подбором последних могут быть осуществлены ситуации, когдаU R , U C и U L существенно неодинаковы. Рассмотрим для случая цепи, в которой U L » 0 (RC – цепь).

А) U C >> U R , тогда из (3) имеем:

i(t) = C dU вх (t)/dt (4)

Отсюда следует, что напряжения на сопротивлении пропорционально производной от входного сигнала:

U R (t) = RCdU вх (t)/dt = t 0 dU вх (t)/dt. (5)

Таким образом, мы приходим к схеме дифференцирующего четырёхполюсника, показанной на рис.2, в которой выходной сигал снимается с сопротивления R.

Б) U R >> U C . В этом случае из (3) получаем: i(t) = U вх (t)/R(6) и напряжение на емкости равно:

U C = 1/RCòU вх (t)dt = 1/t 0 òU вх (t)dt. (7)

Видно, что для осуществления операции интегрирования необходимо использовать RC-цепочку в соответствии со схемой на рис.3.

Для получения как эффекта дифференцирования, так и интегрирования, сигнал надо снимать с элемента, на котором наименьшее падение напряжения. Величина U вых (t) определяется значением постоянной времени t 0 , равной RC для RC-цепочки.

Очевидно, что эффекты дифференцирования и интегрирования в общем случае отвечают, соответственно, относительно малым и большим t 0 .

Условия дифференцирования и интегрирования

Уточним теперь, как связаны условия А и Б, а также использованные выше понятия «малого» и «большого» t 0 с параметрами R, C, L и характеристиками сигнала.

Пусть входной сигнал U вх (t) обладает спектральной плотностью

Тогда при точном дифференцировании для выходного сигнала получим:

откуда следует, что коэффициент передачи идеального дифференцирующего четырёхполюсника (

Рассмотренная нами дифференцирующая цепь (рис.2) имеет коэффициент передачи:

Из сравнения (14) и (15) видно, что рассмотренная нами цепь будет тем ближе к идеальной, чем лучше выполняется условие

wt 0 << 1 (16)

Причём, для всех частот в спектре входного сигнала. Для упрощения оценки в неравенство (16) обычно подставляют максимальную частоту в спектре входного сигнала w m t 0 << 1.

Итак, чтобы продифференцировать некоторый сигнал, необходимо найти его спектральный состав и собрать RC-цепь с постоянной времени t 0 << w m -1 , где w m – максимальная частота в спектре входного сигнала.

Отметим, что для импульсных сигналов верхнюю границу полосы частот можно оценить по формуле (2) w m = 2p/t u , где t u – длительность импульса. Т.о., в этом случае условие дифференцирования запишется в виде

t 0 << t u (17)

Совершенно аналогично можно показать, что для удовлетворительного интегрирования требуется выполнение условия

wt 0 >> 1 (18)

также для всех частот спектра входного сигнала, в том числе и для самой нижней. Аналогично для интегрирования импульсов длительностью t u условие интегрирования запишется в виде

t 0 << t u (19)

Из неравенств (16), (18) следует, что при заданной цепи дифференцирование осуществляется тем точнее, чем ниже частоты, на которых концентрируется энергия входного сигнала, а интегрирование – чем выше эти частоты. Чем точнее дифференцирование или интегрирование, тем меньше величина выходного сигнала.

Прохождение прямоугольных импульсов через RC -цепи

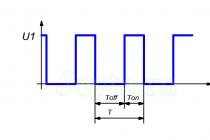
В качестве примера, иллюстрирующего дифференцирование и интегрирование сигналов, рассмотрим отклик RC-цепей, показанных на рис.2 и 3, на прямоугольный импульс. Возьмём цепь, на выходе которой стоит сопротивление (рис.2), найдём осциллограмму выходного напряжения, т.е. вид U R (t). Пусть в момент времени t = 0 на входе возникает скачок напряжения U 0 (рис.4).

В этом случае для 0 < t < t u можно записать уравнение цепи в виде:

U 0 = 1/Còi(t)dt + U R (t). (17)

После дифференцирования получим

dU R /dt + U R /t 0 = 0. (18)

Поскольку ёмкость С не может зарядиться мгновенно, то для t = 0, U R = U 0 всё входное напряжение оказывается приложенным к сопротивлению. С учётом этого начального условия решение уравнения (18) запишется в виде:

Экспоненциальный спад выходного напряжения описывает процесс зарядки ёмкости через сопротивление R и соответствующее перераспределение напряжения между R и C. При этом постоянная времени t 0 характеризует скорость зарядки ёмкости и может быть интерпретирована как время, за которое напряжение U R уменьшится в е раз.

Для t 0 << t u экспоненциальная зависимость становится резче, в результате на выходе наблюдаем короткие импульсы в момент начала и окончания входного воздействия, являющиеся удовлетворительной аппроксимацией производной от входного сигнала (рис.4).

Если выходное напряжение снимается с конденсатора, то для 0 < t < t u получим:

и для t >= t u

Если цепь является интегрирующей, то выполняется неравенство t 0 >> t u , что позволяет использовать разложение экспоненты в ряд Тейлора.

Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C , представленную на рисунке.

Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R . Напряжение на выводах резистора обозначим U R .
Тогда будет иметь место равенство:

Проинтегрируем последнее выражение . Интеграл левой части уравнения будет равен U out + Const . Перенесём постоянную составляющую Const в правую часть с тем же знаком.
В правой части постоянную времени RC вынесем за знак интеграла:

В итоге получилось, что выходное напряжение U out прямо-пропорционально интегралу напряжения на выводах резистора, следовательно, и входному току I in .
Постоянная составляющая Const не зависит от номиналов элементов цепи.

Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения U out от интеграла входного U in , необходима пропорциональность входного напряжения от входного тока.

Нелинейное соотношение U in /I in во входной цепи вызвано тем, что заряд и разряд конденсатора происходит по экспоненте e -t/τ , которая наиболее нелинейна при t/τ ≥ 1, то есть, когда значение t соизмеримо или больше τ .
Здесь t - время заряда или разряда конденсатора в пределах периода.
τ = RC - постоянная времени - произведение величин R и C .
Если взять номиналы RC цепи, когда τ будет значительно больше t , тогда начальный участок экспоненты для короткого периода (относительно τ ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током.

Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость U in /I in ≈ R .
В таком случае выходное напряжение U out будет с допустимой погрешностью пропорционально интегралу входного U in .
Чем больше величины номиналов RC , тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.

В большинстве случаев, переменная составляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const , тогда номиналы RC можно выбирать по возможности большими, но с учётом входного сопротивления следующего каскада.

В качестве примера, сигнал с генератора - положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:
R = 10 kOhm, С = 1 uF. Тогда τ = RC = 10 mS.

В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.
График показывает, что выходное напряжение на уровне постоянной составляющей 0.5в будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её a ), а интеграл константы будет линейной функцией. ∫adx = ax + Const . Величина константы a определит тангенса угла наклона линейной функции.

Проинтегрируем синусоиду, получим косинус с обратным знаком ∫sinxdx = -cosx + Const .
В данном случае постоянная составляющая Const = 0.

Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение.
Интеграл линейного участка функции - парабола. В простейшем варианте ∫xdx = x 2 /2 + Const .
Знак множителя определит направление параболы.

Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.

Рассмотрим в качестве интегратора Операционный Усилитель (ОУ) по схеме, показанной на рисунке.

С учётом бесконечно большого сопротивления ОУ и правила Кирхгофа здесь будет справедливо равенство:

I in = I R = U in /R = - I C .

Напряжение на входах идеального ОУ здесь равно нулю, тогда на выводах конденсатора U C = U out = - U in .
Следовательно, U out определится, исходя из тока общей цепи.

При номиналах элементов RC , когда τ = 1 Sec, выходное переменное напряжение будет равно по значению интегралу входного. Но, противоположно по знаку. Идеальный интегратор-инвертор при идеальных элементах схемы.

Дифференцирующая цепь RC

Рассмотрим дифференциатор с применением Операционного Усилителя.

Идеальный ОУ здесь обеспечит равенство токов I R = - I C по правилу Кирхгофа.
Напряжение на входах ОУ равно нулю, следовательно, выходное напряжение U out = U R = - U in = - U C .
Исходя из производной заряда конденсатора, закона Ома и равенства значений токов в конденсаторе и резисторе, запишем выражение:

U out = RI R = - RI C = - RC(dU C /dt) = - RC(dU in /dt)

Отсюда видим, что выходное напряжение U out пропорционально производной заряда конденсатора dU in /dt , как скорости изменения входного напряжения.

При величине постоянной времени RC , равной единице, выходное напряжение будет равно по значению производной входного напряжения, но противоположно по знаку. Следовательно, рассмотренная схема дифференцирует и инвертирует входной сигнал.

Производная константы равна нулю, поэтому постоянная составляющая при дифференцировании на выходе будет отсутствовать.

В качестве примера, подадим на вход дифференциатора сигнал треугольной формы. На выходе получим прямоугольный сигнал.
Производная линейного участка функции будет константой, знак и величина которой определится наклоном линейной функции.

Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.

U out = RI R = RI C = RC(dU C /dt)

Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определённой степени точно. В идеале это приращение должно стремиться к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.

Наиболее часто дифференцирующие и интегрирующие цепи RC применяют для изменения длины импульса в логических и цифровых устройствах.
В таких случаях номиналы RC рассчитывают по экспоненте e -t/ RC исходя из длины импульса в периоде и требуемых изменений.
Например, ниже на рисунке показано, что длина импульса T i на выходе интегрирующей цепочки увеличится на время 3τ . Это время разряда конденсатора до 5% амплитудного значения.

На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно, так как на выводах разряженного конденсатора оно равно нулю.
Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.

Здесь 5% - величина показательная. В практических расчётах этот порог определится входными параметрами применяемых логических элементов.

Замечания и предложения принимаются и приветствуются!

В дифференцирующей цепи (рис. 11.2, а) постоянная вре­мени должна быть малой по сравнению с длительностью им­пульсов. Эту цепь применяют в тех случаях, когда импульсы сравнительно большой длительности необходимо преобразовать в короткие запускающие импульсы с крутым фронтом. Цепь сохраняет крутой фронт импульса в той же полярности и по су­ществу ведет себя как фильтр верхних частот, ослабляющий низкочастотные и пропускающий высокочастотные составляю­щие импульса.

При подаче напряжения на конденсатор протекающий через него ток пропорционален производной приложенного к конден­сатору напряжения е с:

(11.4)

При малой постоянной времени сопротивление резистора ока­зывается значительно больше реактивного сопротивления кон­денсатора. Поэтому выходное напряжение, равное падению на­пряжения на резисторе, приближенно выражается формулой

(11.5)

На рис. 11.2,6 и в показаны соответственно формы импуль­са на входе и выходе дифференцирующей цепи. От начального момента действия импульса и в течение всей его длительности к входу схемы прикладывается постоянное напряжение. Если при подаче входного импульса конденсатор Ci не был заряжен, то в первый момент через конденсатор, а также через рези стор R1 будет протекать большой ток. Таким образом, на рези­сторе сразу же появляется большое падение напряжения, бла­годаря чему на выходе очень быстро нарастает фронт импульса (рис. 11.2, в). По мере заряда конденсатора протекающий че­рез него ток уменьшается со скоростью, зависящей от постоян­ной времени цепи. При малой постоянной времени конденса­тор быстро заряжается и ток перестает протекать по цепи. Та­ким образом, когда конденсатор полностью заряжен, напряже­ние на резисторе R 1 спадает до нулевого уровня. В момент окончания действия импульса входное напряжение уменьшает­ся до нуля, и конденсатор начинает разряжаться. Ток разряда конденсатора имеет противоположное но сравнению с током за­ряда направление, следовательно, направление тока через рези­стор также противоположно току заряда. Поэтому на выходе теперь появится отрицательный всплеск напряжения.

Рис. 11.2. Дифференцирующая цепь (а) и форма импульса на входе (б) и выходе (в) цепи.

На практике на вход дифференцирующей цепи обычно по­даются импульсы. Если же на вход дифференцирующей цепи подать синусоидальные колебания, то их форма не изменится, но произойдут сдвиг фазы выходного колебания и уменьшение амплитуды этих колебаний на величины, зависящие от частоты входного сигнала. Другой тип дифференцирующей схемы мож­но получить, если C 1 заменить резистором, а R 1 - индуктив­ностью. В такой цепи фактором, определяющим качество диф­ференцирования, является также постоянная времени. Как и в интегрирующей цепи, омическое сопротивление катушки индук­тивности ухудшает характеристики схемы. Поэтому такую цепь применяют довольно редко.

Дифференцирующие цепи используют тогда, когда требуется преобразовать напряжение заданной формы в сигнал ипых , изменяющийся по закону

где - коэффициент пропорциональности.

Простейшая дифференцирующая RС-цепь аналогична интегрирующей RС-цепи и отличается только тем, что выходное напряжения снимается не с конденсатора, а с активного сопротивления (рис. 6.19, а). Напряжение на ее выходе

Напряжение на конденсаторе .

Если т. е. -цепь успешно выполняет дифференцирование только в этом случае.

Оценим приближенно погрешность, вносимую членом , для чего продифференцируем выражение для , считая

Подставив (6.98) в (6.96), получим

Таким образом, для улучшения дифференцирования надо, чтобы

(6.100)

т. е. необходимо уменьшать постоянную времени -цепи ). Это требование противоположно требованию к интегрирующей цепи, где для точного интегрирования увеличивали постоянную времени.

Выходной сигнал в дифференцирующей цепи, так же как и в интегрирующей, уменьшается при повышении точности выполнения соответствующего преобразования. Действительно, уменьшение постоянной времени в дифференцирующей цепи приводит к уменьшению члена , вызывающего погрешность дифференцирования. При этом уровень выходного сигнала снижается пропорционально уменьшению .

При дифференцировании наибольшая погрешность получается в течение времени нарастания (или среза) импульса. Это обусловлено тем, что при этих процессах вторая производная, выражающая скорость изменения крутизны фронта (или среза), имеет наибольшее значение.

Наименьшая погрешность имеет место в те промежутки времени, в которых скорость изменения входного напряжения постоянна.

Рис. 6.19. Дифференцирующая -цепь (а) и диаграммы изменения напряжения на ее отдельных участках (б, в, г)

Выясним возможности и условия дифференцирования -цепью синусоидального изменяющегося напряжения .

При точном дифференцировании этот сигнал должен изменяться по закону

(6.101)

Таким образом, выходное напряжение должно быть сдвинуто по фазе на 90° относительно входного. В реальной RС-цепи амплитуда и фаза отличаются от соответствующих значений идеальной дифференцирующей цепи. Выходное напряжение

а фазовый угол

(6.103)

Для того чтобы иметь возможность дифференцировать синусоидально изменяющееся напряжение частотой , необходимо выполнить условие Однако при этом уменьшается и значение выходного сигнала. Поэтому приходится ограничиваться компромиссным решением, при котором выходной сигнал и фазовая погрешность не выходят за пределы допустимых значений.

Если, например, принять , то фазовая погрешность дифференцирования 14°. Такие фазовые искажения выходного сигнала в ряде случаев общего применения можно считать приемлемыми. При этом значение выходного сигнала мало зависит от , так как да 1, поэтому его можно считать близким к теоретическому.

При дифференцировании импульса активная ширина его спектра ограничена частотой . Если неравенство выполняется при , то оно будет обязательно выполняться и при . Это позволяет исходя из активной ширины спектра определить требования к постоянной времени дифференцирующей цепи:

Для грубой оценки активной ширины спектра при равных длительностях фронта и среза импульса можно использовать приближенное выражение

(6.105)

где для импульсов, у которых , т. е. для наиболее часто встречающихся.

Тогда, подставив в (6.104) значение , получим

Таким образом, постоянная времени дифференцирующей -цепи общего применения должна быть примерно в десять раз меньше активной длительности фронта дифференцируемого импульса.

При дифференцировании однополярного импульса на выходе дифференцирующей цепи образуется двухполярный импульс Следовательно, длительность выходного импульса напряжения одной какой-либо полярности меньше длительности дифференцируемого импульса и рассматриваемая цепь обеспечивает выполнение операции укорочения.

Пусть на входе RС-цепи (рис. 6.19, а) действует идеальный прямоугольный импульс, который приходит в момент времени (рис. ). При этом конденсатор С начинает заряжаться и напряжение на нем изменяется по закону

Зарядный ток , протекающий через сопротивление R, создает на выходе RС-цепи экспоненциальный импульс ивых положительной полярности, который полностью затухает до окончания действия входного импульса. После окончания входного импульса равновесие, достигнутое в цепи , нарушается. Происходит разряда конденсатора через резистор R и источник импульсов. Выходной импульс отрицательной полярности, возникающий при разрядке конденсатора, отличается от рассмотренного только полярностью.

Таким образом, при укорочении прямоугольного импульса на выходе цепи получаются экспоненциальные импульсы напряжения положительной и отрицательной полярности, высота которых равна высоте входных импульсов . Длительность выходных импульсов определяется постоянной времени . Если ее измерять на уровне , то она определяется из выражения

Иногда активную длительность импульса измеряют на уровне :

Постоянную времени дифференцирующей цепи при ее использовании для укорочения импульсов выбирают значительно большей, чем при выполнении операции точного дифференцирования.

Ее значение находят исходя из требуемой активной длительности импульса, определенной на уровне .

В реальных случаях приходится учитывать внутреннее сопротивление источника, к которому рассматриваемая цепь подключена (рис. 6.20, я). При этом характер процессов в -цепи не меняется. Однако увеличение активного сопротивления цепи приводит к возрастанию постоянной времени . Это ограничивает возможность получения коротких импульсов. Кроме того, уменьшаются зарядный и разрядный токи i конденсатора, что приводит к уменьшению выходного напряжения . Максимальное значение выходного напряжения находят из уравнения

Мы имеем полное право перейти к рассмотрению цепей, состоящих из этих элементов 🙂 Этим мы сегодня и займемся.

И первая цепь, работу которой мы рассмотрим – дифференцирующая RC-цепь.

Дифференцирующая RC-цепь.

Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор 🙂 И выглядит она следующим образом:

Работа данной схемы основана на том, что ток, протекающий через конденсатор , прямо пропорционален скорости изменения напряжения, приложенного к нему:

Напряжения в цепи связаны следующим образом (по закону Кирхгофа):

В то же время, по закону Ома мы можем записать:

Выразим из первого выражения и подставим во второе:

При условии, что (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:

Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала.

Но возможен еще и другой случай, когда title="Rendered by QuickLaTeX.com" height="22" width="134" style="vertical-align: -6px;"> (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:

То есть: .

Можно заметить, что условие будет лучше выполняться при небольших значениях произведения , которое называют постоянной времени цепи :

Давайте разберемся, какой смысл несет в себе эта характеристика цепи 🙂

Заряд и разряд конденсатора происходит по экспоненциальному закону:

Здесь – напряжение на заряженном конденсаторе в начальный момент времени. Давайте посмотрим, каким будет значение напряжения по истечении времени :

Напряжение на конденсаторе уменьшится до 37% от первоначального.

Получается, что – это время, за которое конденсатор:

• при заряде – зарядится до 63%
• при разряде – разрядится на 63% (разрядится до 37%)

С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи 🙂

Теоретические аспекты функционирования цепи мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:

А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):

Что же мы тут видим?

Большую часть времени напряжение на входе неизменно, а значит его дифференцаил равен 0 (производная константы = 0). Именно это мы и видим на графике, значит цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно . Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:

При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора:

В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике 🙂

Будем увеличивать сопротивление резистора, что и приведет к росту :

Тут даже не надо ничего комментировать – результат налицо 🙂 Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям .

Запишем выражения для вычисления тока и напряжения данной цепи:

В то же время ток мы можем определить из Закона Ома:

Приравниваем эти выражения и получаем:

Проинтегрируем правую и левую части равенства:

Как и в случае с дифференцирующей RC-цепочкой здесь возможны два случая:

Для того, чтобы убедиться в работоспособности цепи, давайте подадим на ее вход точно такой же сигнал, какой мы использовали при анализе работы дифференцирующей цепи, то есть последовательность прямоугольных импульсов. При малых значениях сигнал на выходе будет очень похож на входной сигнал, а при больших величинах постоянной времени цепи, на выходе мы увидим сигнал, приближенно равный интегралу входного. А какой это будет сигнал? Последовательность импульсов представляет собой участки равного напряжения, а интеграл от константы представляет из себя линейную функцию (). Таким образом, на выходе мы должны увидеть пилообразное напряжение. Проверим теоретические выкладки на практике:

Желтым цветом здесь изображен сигнал на входе, а синим, соответственно, выходные сигналы при разных значениях постоянной времени цепи. Как видите, мы получили именно такой результат, который и ожидали увидеть 🙂

На этом мы и заканчиваем сегодняшнюю статью, но не заканчиваем изучать электронику, так что до встречи в новых статьях! 🙂